OK, sometimes there are other rewards. A retiring college professor insisted on paying me for her retirement plan so I negotiated dinner with her at a new pizza place I had wanted to try. (Yes, I work for pizza.) A podcast producer interviewed me and afterward sent a really nice set of engraved kitchen knives. My wife is an amazing cook. She is also an MBA but opening those knives was the first time in two decades that she has shown any interest whatsoever in my retirement planning hobby.
Back to learning stuff, I’ll wrap up the year by sharing a few of the things I learned in 2018 that you might find useful.
I spent most of this year co-authoring research with Neville Frances, a UNC econometrician. The first thing I learned was that a research project can take four times as long as you expect and dramatically impact the amount of time you have to write blog posts. I hope to do much better next year.
I learned that a lot of poor research is published. I was already aware that a lot of excellent research is available in the retirement finance field but also a lot that is questionable. When I discussed this with my co-author, he shrugged and told me that’s true of all of economics. So, I checked with my son, a medical researcher. He confirmed that he runs across a lot of junk in that field, too.
If you read something in a peer-reviewed journal, be skeptical. If you read it elsewhere, be very skeptical. I’m planning a column on the topic for early next year but Francois Gadenne has already published his thoughts.[1]
Most papers are essentially arguments. I find one of the problems with reading papers is that many people can’t logically deconstruct an argument. I read a paper this year, for example, that made several claims but provided no evidence to support any of them. If the basic argument is flawed then discount the research.
If you’re interested in analyzing arguments, my friend, Dr. Walter Sinnott-Armstrong, created an excellent, free video class at Duke University[2] and he has written a couple of books on the topic with Think Again perhaps the more readable.[3,4]
I learned the extent to which sustainable withdrawal rate (SWR) is explained by sequence of returns as opposed to the portfolio returns, themselves. "Big Ern" at EarlyRetirementNow.com found a convincing way to explain it.[5] He found that "knowing only the average returns over the next 30 years is not very informative."
But he also found that for a 30-year retirement, nearly all (close to 96%) of the variation in the sustainable withdrawal rate is explained by the average returns of six five-year windows. The average return for years 0 to 5 explains about 29% of SWR variance and the average return for years 5 to 10 explains another 19%. Explanatory power declines further in subsequent windows and totals about 0.96.
(If terms like "regression testing" and "R-squared" don't frighten you away, I highly recommend the post or any other on his blog.)
The simple takeaway here is that when you spend from a volatile portfolio, the long-term returns matter very little compared to the sequence of those returns. Don't worry about whether your portfolio will earn an average 8% a year but about when the bad years will occur. (Later is better.)
This doesn't mean, however, that once we survive the first five years of retirement sequence risk goes away.
I used Ern’s spreadsheet to estimate that returns for the first four years of a retirement with 20 years remaining have about the same explanatory power as the returns for the first five years when 30 years remain. The explanatory power of the returns for the first two years of a retirement with 10 years remaining is about the same as these. Sequence risk becomes “compressed” but it never goes away entirely.
If we successfully navigate the first five years of portfolio returns then we still have to negotiate the next five and eventually the next two. There's no reason to expect that if you make it through the first 5 years of retirement that your risk will simply disappear.
I learned that many Monte Carlo models are poorly designed. I also learned that many advisors who use them don’t really understand the technique and by the time they explain the results to the typical client, most of its value is lost. Although I still consider MC an extremely valuable tool, I'm now cautious about recommending it because I'm not confident that it will be used and interpreted correctly.
I learned from Zvi Bodie that probability of ruin (or probability of shortfall) is a problematic metric not only because it measures the probability of a shortfall while ignoring the magnitude of the loss but also because it ignores utility. He explained this in terms of Arrow-Debreu contingent claim state prices, which probably makes as much sense to my readers as it did to me when I first read his explanation.[6] I had to learn about Arrow-Debreu before I could even have a discussion. A-D won't interest normal people but I found it pretty exciting. It even gave me some insight into the Black-Scholes model.
[Tweet this]Having less confidence when I retired would have served me well.
Simultaneously, I was learning a great deal about MC from my econometrician co-author and it became clear from our work that using MC to measure probability of ruin has even more problems than using the historical probability of ruin. (Probability of ruin isn't a "robust" model metric.) We don't understand the process that determines the sequences and we don't have enough independent 30-year historical sequences to provide insight, so we don't really know how to model sequence of returns. In turn, I no longer have confidence in analyses that measure Monte Carlo model results using probability of ruin as the metric.
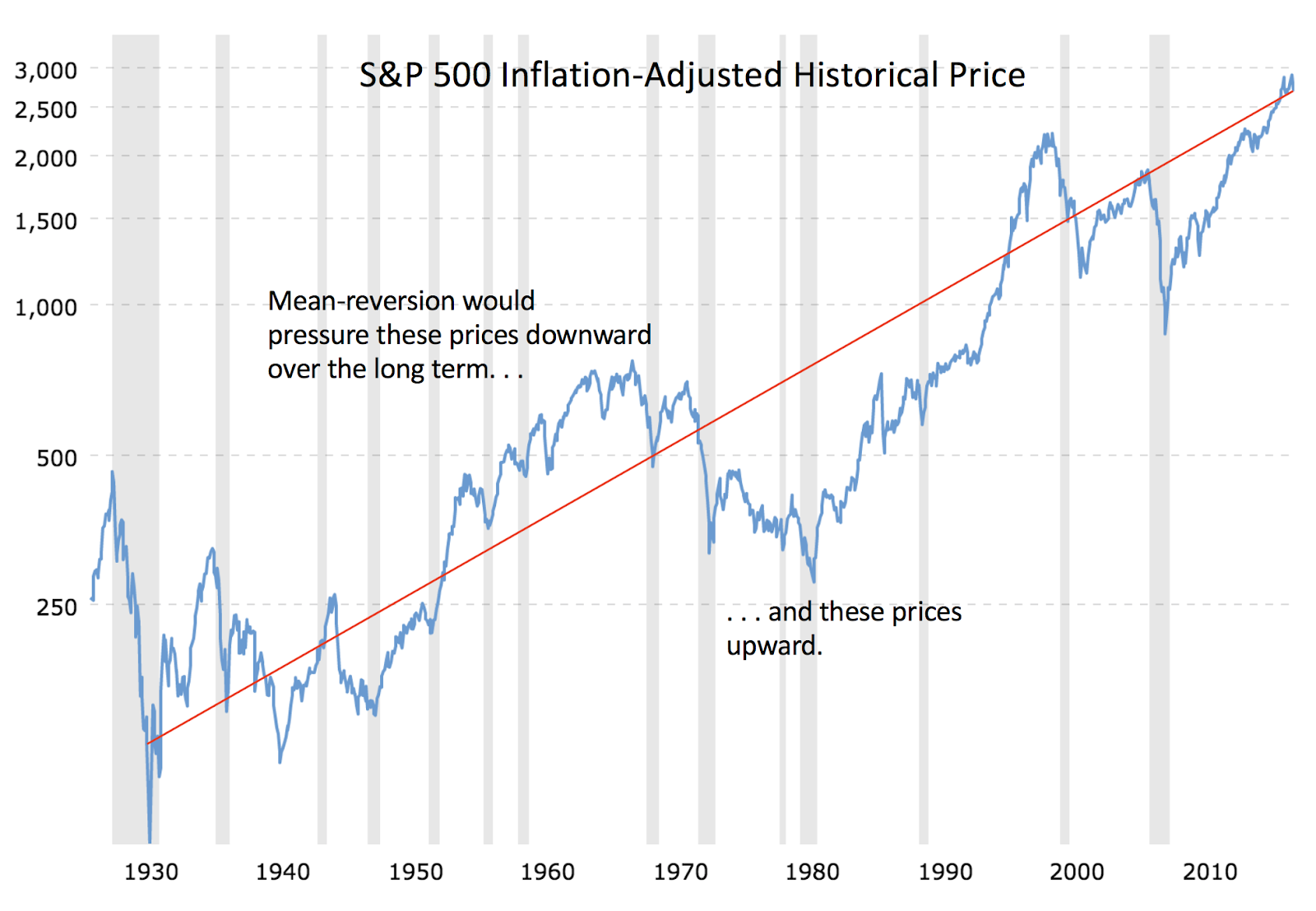
I learned that there is no consensus among economists as to whether stock returns mean-revert or, even if they do, if that would imply that stocks become safer the longer we hold them. (See Mean Reversion of Equity Returns and Retirement Planning.)
Lastly, I learned that I'm not the only one concerned about retirement planning for unwealthy households. Wade Pfau, Steve Vernon and Joe Tomlinson addressed this problem in a hefty tome entitled, "Optimizing Retirement Income by Integrating Retirement Plans, IRAs and Home Equity." You might want to read Vernon's shorter discussion of part of this work referred to as the "Spend Safely in Retirement Strategy" here[7] in which he concludes:
The "Spend Safely in Retirement" strategy represents a straightforward way for middle-income workers with between $100,000 and $1 million in savings to generate a stream of lifetime retirement income without purchasing an annuity and without significant involvement from financial advisers. This group might represent as many as half of all workers age 55 and older.This is hardly an ideal retirement finance strategy but retirees with limited resources and no access to a good financial adviser might have difficulty finding a better one and I think that was the goal.
So, that's some of the important stuff I learned in 2018. Ironically, the more I learn about retirement finance the less certain I become about what I thought I knew. Being less confident back when I retired would have served me well.
Wishing you a happy and enlightening 2019!
REFERENCES
[1] How to Read Research Papers With a Discerning Eye: Take the Best and Leave the Rest by Francois Gadenne.
[2] Think Again I: How to Understand Arguments, Coursera.
[3] Understanding Arguments by Walter Sinnott-Armstrong.
[4] Think Again by Walter Sinnott-Armstrong.
[5] The Ultimate Guide to Safe Withdrawal Rates – Part 15: More Thoughts on Sequence of Return Risk, EarlyRetirementNow.com
[6] An Analysis of Investment Advice to Retirement Plan Participants by Zvi Bodie. (see footnote 10)
[7] Meet the "Safe Spending in Retirement Strategy" by Steve Vernon.